Derivation of Combined Angle

Abstract: Derivation of combined angle may become useful when you want to know the magnitude and direction of force due to bend in both XY and XZ plane. For eg in design of bend in pipeline.

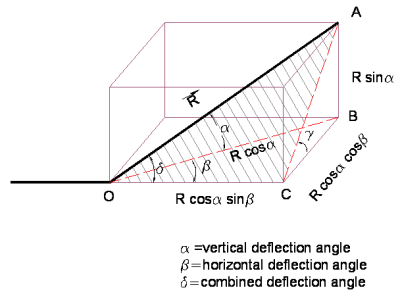
Let us consider a straight line which deflects at O along OA as shown in the figure. The deflection angles are also shown in the figure.

Let R be the position vector of A. OB is projection of OA on XY plane and AB is projection of OA on a plane parallel to YZ plane. Similarly, OC is projection of line OB in X axis and BC is projection of OB on axis parallel to Y axis.

From figure it can inferred that

OB=R cosα

AB=R sinα

OC=OB cosβ = R cosα cosβ

BC= OB sinβ =R cosα sinβ

Therefore, the position vector of A is OA which is given by

R=|R| (cosα cosβ i + cosα sinβ j + sinα k )

And the unit vector along R is given by

r= (cosα cosβ i + cosα sinβ j + sinα k )

Now the combined deflection angle is given by

r . i =|r| |i| cosδ

Or, r . i =1*1 cosδ

Or, cosδ = cosα cosβ+0+0

Or, δ =cos^-1(cosα cosβ)

The angle δ lies in the plane OAC. This plane is shown in the figure in hatch line.

Forces

If F be the magnitude of force due to the deflection δ (e.g. deflection in pipeline) then the vertical and horizontal component of this force is given by,

F_x1 =F r . i =F cosα cosβ

F_x2 =F r . j =F cosα sinβ

F_x =F

=F cosα

F_y =F r . j

=F sinα